Представьте: сидите на паре, погрязнув в огромных формулах, нить рассуждений потеряна, и вы уже не понимаете, о чем идет речь. Знакомое ощущение? Вот именно. Чтобы вы не упускали самую суть вещей, мы подготовили объяснение некоторых непростых тем простыми словами.
А чтобы вообще всегда были в курсе событий, подписывайтесь на наш телеграм-канал.
Что такое матрицы
Сегодня поговорим о матрицах. Пройти через эту тему предстоит, наверное, всем студентам, изучающим высшую математику (линейную алгебру, точнее говоря).
Именно с матриц начинается большинство курсов высшей математики. И пусть вас не пугает слово высшая. На самом деле, все не так страшно. Смотрите сами.
Матрица – это таблица. Таблица чисел, или букв, за которыми скрываются числа.
Матрицы могут быть разного размера: квадратные, прямоугольные, есть матрицы, состоящие всего из одной строки или одного столбца (горизонтальные и вертикальные).
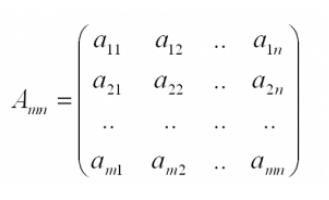
Размер матрицы определяется количеством строк m и столбцов n. Номера строк и столбцов – буквами i и j соответственно.
Еще у матрицы есть не только строки и столбцы, но и диагонали. Элементы матрицы, для которых i=j (a11, a22, .. ) образуют главную диагональ матрицы, и называются диагональными.
А теперь, что еще нужно в первую очередь знать о работе с матрицами.
Как складывать матрицы
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера.
Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример.
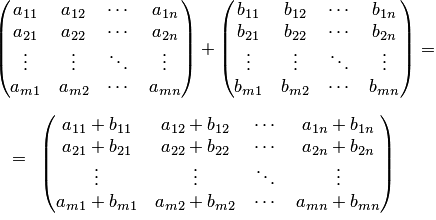
Вычитание выполняется по аналогии, только вместо плюса пишем минус.
Как умножать матрицы
Во-первых, запомните: матрицу А можно умножить на матрицу B, только если если число столбцов матрицы А равно числу строк матрицы В.
При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м.
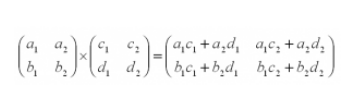
Вместо букв в матрице могут стоять реальные числа. Вот что получится, если умножить такие матрицы:
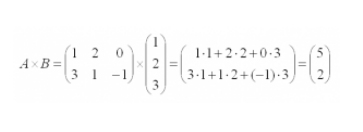
Что такое транспонированная матрица
Транспонировать матрицу – значит поменять строки и столбцы местами.
Вот как будет выглядеть матрица из самого первого примера, если ее транспонировать. Сама операция транспонирования обозначается индексом Т.
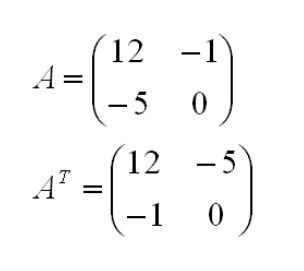
Что такое детерминант матрицы
Детерминант – это определитель – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.К счастью, вычислять определители матриц больших размеров на практике приходится редко. А если часто, то с этим справятся специалисты студенческого сервиса. Обращайтесь, они помогут!












